[Statistique] Paradoxe de Simpson

Aucun rapport avec la série, mais je trouve ce truc vraiment intéressant et perturbant parce que totalement contre-intuitif!
J’ai vu pas mal de cas d’exemples ces derniers temps et j’avais envie d’en parler … bon j’aurais mis le temps à le poster mais mieux vaut tard que jamais

Je reprends toujours l’article sur wikipedia et ensuite vous aurez quelques vidéos et petits liens !
Le paradoxe de Simpson ou effet de Yule-Simpson est un paradoxe statistique décrit par Edward Simpson en 1951 et George Udny Yule en 1903, dans lequel un phénomène observé dans plusieurs groupes s’inverse lorsque les groupes sont combinés.
Ce résultat qui semble impossible au premier abord est lié à des éléments qui ne sont pas pris en compte (comme la présence de variables non indépendantes ou de différences d’effectifs entre les groupes, etc.) est souvent rencontré dans la réalité, en particulier dans les sciences sociales et les statistiques médicales.
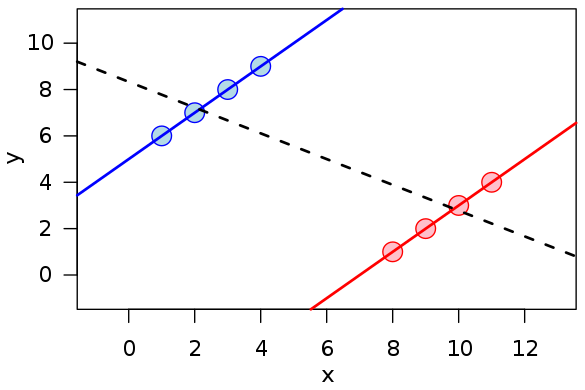
– Wikipedia
Illustration du paradoxe de Simpson pour un échantillon de données : alors que des tendances positives apparaissent dans les échantillons rouge et bleu, l’union des deux échantillons présente une tendance inversée, négative (représentée par la droite pointillée noire).
Résultats scolaires et pratique sportive
Pour expliquer le paradoxe de Simpson, imaginons que l’on mesure la performance scolaire de différents élèves en fonction de la quantité de sport pratiqué.
Supposons que l’on obtienne les résultats présentés dans le graphique en tête de cet article : l’axe horizontal x (abscisse) représente la quantité de sport pratiqué (par exemple en heures par semaine) et l’axe vertical y (ordonnée) représente la performance scolaire (par exemple, la moyenne des notes sur 10).
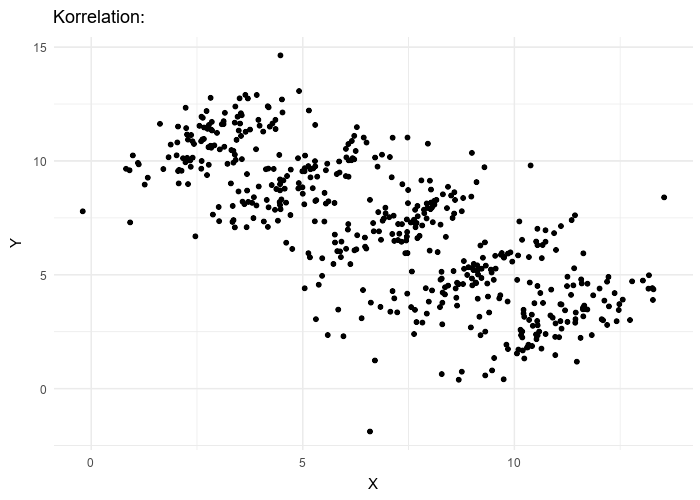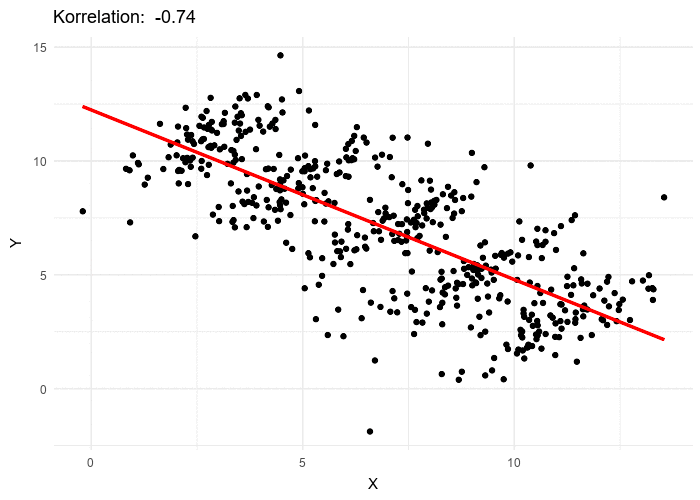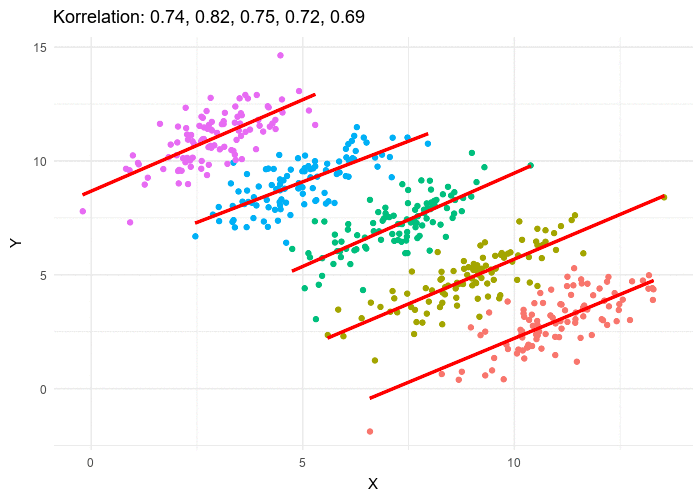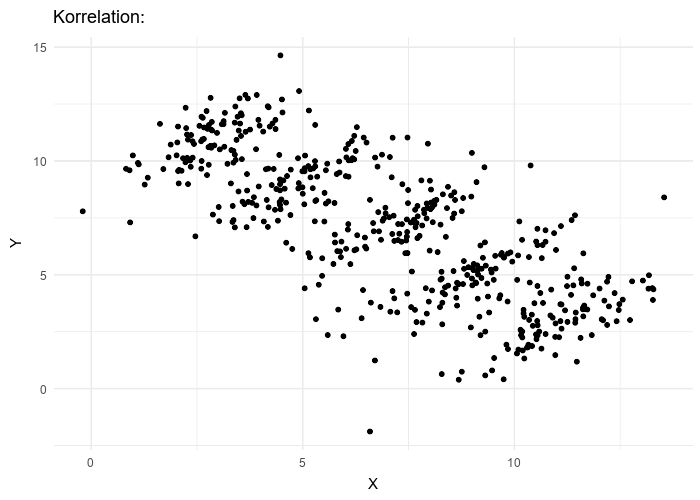
Dans cet exemple imaginaire, on voit que parmi les élèves « bleus » ceux qui pratiquent davantage de sport sont meilleurs à l’école et il en est de même dans le groupe « rouge ».
Pourtant, quand on combine les deux groupes on a une relation inversée qui semble indiquer que plus on pratique de sport (x élevé), moins on obtient de bonnes performances scolaires (baisse sur l’axe y) : l’observation des deux groupes combinés semble contredire ce qu’on a observé dans chacun des groupes.
Cet exemple-jouet illustre l’existence de différences entre les groupes (bleu et rouge) dont on n’a pas tenu compte dans l’analyse.
En les négligeant, on peut aboutir à des conclusions qui semblent contradictoires.
C’est un exemple du paradoxe de Simpson.
Contributeurs de Wikipédia
Pour illustrer ce paradoxe de manière plus détaillée, considérons deux contributeurs de Wikipédia : Lisa et Bart.
La première semaine, Lisa améliore 60 % des articles qu’elle modifie alors que Bart améliore 90 % des articles qu’il modifie.
La deuxième semaine, Lisa n’améliore que 10 % des articles et Bart s’en tient à un score de 30 %.
Les deux fois, Bart obtient un meilleur score que Lisa. Mais lorsque les deux actions sont combinées, Lisa a amélioré un plus grand pourcentage que Bart : elle a amélioré un peu plus de 55 % des articles qu’elle a modifiés alors que Bart n’en a amélioré même pas 36 %.
Le résultat au bout des deux semaines ne peut être déduit des seuls quatre premiers pourcentages car il dépend du nombre de pages modifiées par chaque contributeur.
Il faut donc disposer de ces nombres pour élucider ce paradoxe :
La première semaine, Lisa modifie 100 articles.
Elle améliore donc 60 articles. Pendant ce temps, Bart s’occupe de 10 articles et en améliore ainsi 9.
La deuxième semaine, Lisa ne modifie que 10 articles et n’améliore qu’une seule page.
Bart modifie 100 articles et en améliore 30.
Quand le résultat à la fin des deux semaines est combiné, on constate que les deux contributeurs ont modifié le même nombre d’articles (110) mais que Lisa en a amélioré 61 alors que Bart n’en a amélioré que 39.
| Semaine 1 | Semaine 2 | Total | |
|---|---|---|---|
| Lisa | 60/100 = 60 % | 1/10 = 10 % | 61/110 = 55,45 % |
| Bart | 9/10 = 90 % | 30/100 = 30 % | 39/110 = 35,45 % |
Il apparaît que les deux données, séparées, soutiennent une hypothèse donnée mais, une fois rassemblées, démontrent l’hypothèse inverse.
D’une manière plus formelle :
La première semaine :
Sa(1)=60%~ — Lisa améliore 60 % des articles qu’elle modifie
Sb(1)=90%~ — Bart améliore 90 % des articles qu’il modifie
La notion de succès est associée à Bart.
La deuxième semaine :
Sa(2)=10%~ — Lisa améliore 10 % des articles qu’elle modifie
Sb(2)=30%~ — Bart améliore 30 % des articles qu’il modifie
Le succès est ici encore attribué à Bart.
Dans les deux cas, Bart a un meilleur pourcentage d’amélioration.
Mais en combinant les deux résultats, nous voyons que Lisa et Bart ont modifié 110 articles.
On établit ainsi :
Sa = 61 / 110 — Lisa a amélioré 61 articles.
Sb = 39 / 110 — Bart en a amélioré seulement 39.
Sa > Sb — Lisa repasse en tête (hypothèse opposée)
Bart est meilleur pour chaque semaine mais globalement plus mauvais, d’où le paradoxe.
Les bases mathématiques du paradoxe sont sans équivoque.
Si Sb(1) >Sa(1) et Sb(2) >Sa(2), on sent que Sb doit être plus grand que Sa.
Mais si des pondérations différentes sont utilisées pour obtenir le score final de chaque personne, alors cette tendance s’inverse.
Le premier score de Lisa est pondéré : 100 / 110 de même pour Bart : 10 / 110.
Mais ces poids sont inversés par la suite.
Sa = 100 / 110 Sa(1) + 10 / 110 Sa(2)
Sb = 10 / 110 Sb(1) + 110 / 110 Sb(2)
Finalement, la question est de savoir qui est le plus efficace.
Lisa paraît supérieure grâce à son succès global qui est le plus grand.
Mais il est possible de reformuler la situation afin que Bart apparaisse plus efficace.
Supposons que le cas se présente comme suit :
La première semaine, Lisa et Bart corrigent des erreurs simples, par exemple des coquilles.
Mais la deuxième semaine, ils s’attaquent à la neutralité des articles, tâche qui nécessite une réflexion plus poussée.
Maintenant, on remarque que Bart s’en sort mieux que Lisa dans la correction de la neutralité.
Malgré ses interventions, Bart est globalement moins efficace que Lisa mais la grande différence vient du fait que Lisa s’est principalement occupée de tâches triviales de la première semaine alors que Bart a fait un peu de tout, et surtout des neutralisations plus complexes.
On remarque ainsi à travers cet exemple que le contexte est important pour qualifier la notion de succès, concept qui peut être trompeur si l’on s’en tient aux chiffres
Traitement des calculs rénaux
Un exemple réel provenant d’une étude médicale sur le succès de deux traitements contre les calculs rénaux permet de voir le paradoxe sous un autre angle.
Cette table montre le succès des traitements A et B pour soigner petits et gros calculs :
Succès en fonction de la taille des calculs
| petits calculs | gros calculs | ||
|---|---|---|---|
| Traitement A | Traitement B | Traitement A | Traitement B |
| 93 % (81/87) | 87 % (234/270) | 73 % (192/263) | 69 % (55/80) |
Dans les deux cas, le traitement A est plus efficace.
Toutefois, si l’on construit un résultat global en additionnant naïvement les traitements de petits et gros calculs, on trouve que B est plus efficace.
Taux de succès (succès/total)
| Traitement A | Traitement B |
|---|---|
| 78 % (273/350) | 83 % (289/350) |
Ce qui crée le paradoxe, et l’impression erronée que B est globalement plus efficace, c’est que le traitement A a été donné beaucoup plus souvent pour les gros calculs, qui sont plus difficiles à soigner.
Le rebroussement de cette inégalité, qui conduit au paradoxe, se produit à cause de deux effets concurrents :
- La variable supplémentaire (ici la taille des calculs) a un impact significatif sur les rapports, elle a une influence en même temps sur le choix du traitement (les calculs de taille élevée ont été plus souvent traités par le traitement A) et sur le résultat du traitement (les calculs de taille élevée sont plus difficiles à soigner). Cette variable est appelée facteur de confusion
- Les tailles des groupes qui sont combinés quand la variable supplémentaire est ignorée sont très différentes.
(ils se rejoignent un peu cela dit…)
Un magnifique cas de paradoxe de Simpson a récemment été repéré par @jsm2334 dans les données d'hospitalisations Covid israéliennes : https://t.co/po2nDQaBXf
Oui, le vaccin protège contre les hospitalisations, mais il faut prendre en compte un facteur de confusion.#CovidTL
— Tania Louis (@SciTania) August 22, 2021
« 60% des hospitalisations en Israël concernent des vaccinés -> le vaccin ne fonctionne pas ! »On voit beaucoup cet argument en ce moment. Ça paraît logique non ? Simple, solide.
Et bien… si vous pensez ça méfiez-vous de votre instinct.#ParadoxeDeSimpson
Thread pic.twitter.com/kJodPHNP2o— Nicolas Jacob (@Nicolas_Jacob_) August 19, 2021
- Une lampe « planètes » - 23/03/2025
- Sais-tu ce que signifie le mot « Manga » ? - 20/03/2025
- Ali Hazelwood – Check & Mate - 15/03/2025




![[Statistiques, Psychologie] Les biais](https://www.geek-otaku-news.com/wp-content/uploads/2022/07/biais-390x205.jpg)